Condensed Matter Physics Group
Condensed Matter
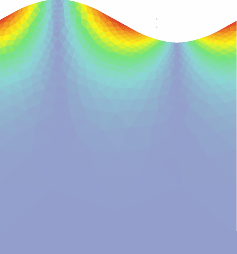
P. Patrício et al. Phys. Rev. Lett. 88 2002
The use and understanding of matter in the condensed state goes back to the beginning of civilization. Its impact was such that the material that dominated the technology was used by historians to name the corresponding period throughout pre-historical times. By the end of the nineteenth century thermodynamics, hydrodynamics and elasticity provided a complete static and dynamic description of the macroscopic properties of matter. With the quantum revolution and the development of new experimental probes that established the atomic nature of matter a new branch of physics was born. The quantum properties of matter were studied with emphasis on the electronic band structure of solids. This programme continues today with studies of superconductivity and the quantum Hall effect in conventional solid state physics.
More recently new paradigms were introduced in condensed matter. The understanding of fluctuations at all length scales in critical phenomena has turned a hopeless non-analytic problem into one of the most profound and elegant physical theories, the renormalisation group theory. This has led to the notions of scaling and universality, and the concepts of broken symmetry and order parameters emerged as unifying theoretical concepts. These advances provided a theoretical framework to describe condensed matter phases ranging from periodic solids to simple and complex fluids, such as liquid crystals, polymers and colloidal dispersions. The field of soft matter includes the study of these so-called soft materials and statistical problems such as phase transitions and critical phenomena.
Macroscopic bodies, such as solids and liquids, are studied by looking at their microscopic interactions and determining how these produce effects at larger length scales. What makes this study difficult is that it is an attempt to solve a many-body problem where large numbers of particles are moving and interacting with one another. Quantum and classical mechanics, including hydrodynamics, coupled with electromagnetic forces (the main interaction between atoms) can give an "exact" description of the dynamics of the phenomena we are interested in, but the equations are so formidable as to be intractable. Therefore, a coarse-grained description is often sought through the methods of statistical physics.
Though condensed matter physics began as a study of matter in its solid state, theorists are currently working on expanding the range of what is known of matter in its condensed state. Research into topics such as nonlinear optics, new man-made materials, systems with quenched disorder and protein physics is dissolving the boundaries between physics and other sciences, from chemistry to biology. In addition, research is being pursued on complex systems in areas such as epidemiology and linguistics.
Ordered Phases and Critical Phenomena
The most spectacular behaviour of spontaneous order in macroscopic systems is displayed by superfluids and superconductors. In these systems, a large fraction of the particles (atoms in superfluids and electron pairs in superconductors) is in the ground state (the state with the lowest energy) and this involves the coherent behaviour of an enormous number of particles; an immediate consequence of this collective organisation at the macroscopic level is the absence of friction in superfluids and of resistence in superconductors.
That most systems exhibit different phases, characterised by different types of order or symmetry is a well known fact. The existence of water, steam and ice is not only familiar but it was essential to the appearance of life on earth. It is also well known that these phases may be transformed: the melting of ice, the condensation of steam or the evaporation of water are as familiar as the phases themselves. Less familiar is the fact that steam and water become indistinguishable at the critical point, that occurs at a temperature of 647 K and a density of 0.323 g/cm3.
Criticality has a very precise meaning in equilibrium systems. It is used in connection with continuous phase transitions and is characterised by coupled fluctuations from microscopic to macroscopic length scales. These fluctuations appear as bubbles of gas in the liquid phase or droplets of liquid in the gas phase. Exactly at the transition there are bubbles and droplets of all sizes, from a molecular scale up to the system size. Away from the transition the surface tension renders the bubbles and droplets unstable. At the transition, however, the liquid and the gas become identical and the surface tension vanishes allowing fluctuations at all length scales. As a consequence a local distortion propagates throughout the entire system and the system becomes critical in the sense that all of its components influence each other.
Examples of continuous transitions may be found in fluids and magnets and include the famous Bose-Einstein condensation.
New man made materials
Recently developed laboratory techniques and theoretical methods have enabled the manufacture or the computer simulation of matter exhibiting new types of order. Some of the most spectacular advances made in this direction have been in materials science, where the pace of technological advance is such that materials can be grown atom by atom or, on the other extreme, on the scale of micrometers using colloidal particles as the building blocks.
Physicists are now able 'order up' totally new material structures, on scales ranging from nano to mesoscopic dimensions and then proceed to explore their structural and electronic properties. As a result a whole new field of quantum physics has appeared – the physics of nanostructures – where new phenomena, many with obvious technological applications, are being discovered almost daily. New technological advances have also allowed physicists to manipulate colloids in such a way that their effective interactions can be controlled in detail. In many cases these interactions differ in fundamental ways from atomic interactions, paving the way for the assembly of new structures that cannot be found in the realm of atomic materials.
Adapted from
Principles of Condensed Matter Physics, P.M. Chaikin and T.C. Lubensky, Cambridge University Press, 2000.
[ Related sites ]
Press releases of the Nobel prizes awarded to Ken Wilson and P.-G. de Gennes for their contribution to the understanding of critical phenomena and complex fluids, respectively.
[ Further reading ]
The Theory of Critical Phenomena: An Introduction to the Renormalization Group, J.J. Binney, N.J. Dowrick, A.J. Fisher and M.E.J. Newman, Oxford University Press, 1992.
